Basic Arithmetic
Before delving into the depths of algebraic concepts, one should familiarize themselves with basic arithmetic. Some common forms of arithmetic that one may hear of are addition, subtraction, multiplication, and division. We will go over these now.
Addition
Consider a situation where you have \(2\) apples. Your best friend then gives you \(3\) apples. You now have \(5\) apples. This is the basic law of addition. The numbers you are "adding" together are \(2\) and \(3\) and number you get, namely \(5\), is the combined version or sum of these two numbers. In the language of mathematics, this operation would look like \[2+3=5\text{.}\] It is read as "two plus three equals five" in terms of english, where \(+\) is the plus sign and \(=\) is the equals sign.
Addition comes with a few basic properties which are taken as definition.
The first property of addition is that two numbers added together generate the same result when the order of addition is flipped. This property is known as commutative property. Like our previous example, say you instead started with \(3\) apples. Now your best friend gives you \(2\) apples. You still have \(5\) apples even though the order of addition is swapped. So we can safely say \(2+3\) is the same as \(3+2\)
The second property of addition is that when more than two numbers are added together, the order in which addition is performed does not matter. This property is known as associative property. Say your other friend gives you \(4\) more apples on top of the \(5\) you already have. You now have \(9\) apples since \(5+4=9\). However, in a different situation say you recieved the \(4\) apples before the \(3\) that your best friend gave you. You will still end up with \(9\) apples in the end. Hence, we can see that \((3+2)+4\) is the same as \((3+4)+2\).
You may be wondering the use of the parentheses in the expressions above. The parentheses indicate which operation should be performed first. For example, consider the expression \((2+4)+6\). The expression within the parentheses should be evaluated first, in this case \(2+4=6\). Then we combine that with the rest of the expression outside of the parentheses. So overall we get, \[(2+4)+6=6+6=12.\] The associative property states that these parentheses can be placed anywhere in an expression of purely addition and the result will remain the same.
The third property is known as the identity property. It states that the number \(0\) added to any number will result in that same number. For example \(9+0=9\). We can make sense of this intuitively by going back to the example with the apples. Say you now have \(9\) apples and nobody else gives you any more apples. You will have \(9\) apples indefinitely.Subtraction
Say you have \(5\) apples and you give your best friend \(1\) apple. You now have \(4\) apples left. This is the principle of subtraction. It is the operation which signifies the removal of things from something else. In the language of mathematics this situation is written as \[5-1=4.\] This is read as "five minus one equals four."
Unlike addition, subtraction is what is known as anticommutative. That is, changing the order of subtraction will change the sign of the answer. But hold on, lets back up a bit. Thus far, we have used real life objects to intuitively understand basic arithmetic. In the world of addition this makes sense, but in the world of subtraction things get weird. Let's consider a situation where you have \(3\) apples (I'll stop with the apples soon) and you give away \(4\), how many apples would you have left? As you might see, this doesn't make sense. How could we give away the extra apple that we do not have. We can't realistically, but in the world of math we can!
So far we have been dealing with positive integers and the number \(0\), which goes like \[0,1,2,3,\dots\] These are known as the counting numbers. But are there more number systems? Of course there are. There are potentially an infinite amount number systems actually, but that is beyond the scope of what we are talking about. Going back to our last example, how can we go beyond \(0\)? We define what is known as the negative integers. The negative integers go like \[-1, -2, -3, \dots\] Of course, putting these number systems together we achieve the number system known as the integers. They are \[\dots ,-3,-2,-1,0,1,2,3,\dots\] These are the numbers that will allow us to take \(4\) away from \(3\), or in the language of mathematics find \(3-4\). So let's see what we get! Take a look at the diagram below to illustrate this.
 We start at \(3\), go \(4\) spaces in the negative direction and end up at \(-1\). Thus we see that \(3-4=-1\).
We start at \(3\), go \(4\) spaces in the negative direction and end up at \(-1\). Thus we see that \(3-4=-1\).
Additionally, earlier it was mentioned that subtraction is anticommutative. This means that switching the order of subtraction will append a minus sign to the answer. Let's see this in action and start with the expression \(4-3\) which we know evaluates to \(1\). But now let's switch the order of subtraction to get \(3-4\). We have already seen this and know that it evaluates to \(-1\). From this, it can be seen that the two answers only differ by a minus sign. Of course this is not a formal proof, so take it as definition for now.
Contrary to addition, subtraction is not associative. This means that the order in which subtraction is written matters. Consider the expression \((10-4)-3\) which evaluates to \(3\). However switching the order to get \(10-(4-3)\) evaluates to \(9\). Since we have found a counter example to subtraction being associative, then it is automatically disproven and false. This notion of true and false will be discussed later when we go over basic logic.
Multiplication
Multiplication is also known as repeated addition. Let's say you wanted to add the number \(5\) to itself \(5\) times. This would look like \[5+5+5+5+5=25.\] While this is okay to write out, what if instead you wanted to add \(5\) to itself \(100\) times? Would you really want to write that out. Likely not. Instead we change our notation. We shall denote the number we want to add to itself as the multiplicand and the number of times we want to add said number to itself as the multiplier. So an expression containing mulitplication would look like \[\text{multiplicand} \times \text{multiplier}.\] Sometimes instead of writting the \(\times\) symbol, people will use the \(\cdot\) symbol to denote mulitplication. This would look like \[\text{multiplicand} \cdot \text{multiplier}.\] The operation of mulitplication is called a product. Let's start off with a basic example!
Example 1 | Find \(2 \times 3\).
Solution: In this expression, the multiplicand is \(2\) and the multiplier is \(3\). So, we need to find what \(2\) added to itself \(3\) times evaluates to. From our knowledge of addition, we find \(2+2+2=6\). Thus \(2 \times 3 = 6\)
We will now go over the fundemental properties of mulitplication.
The first property is that multiplication is commutative, that is switching the order does not change the result.
The second property is that multiplication is associative, that is the order in which mulitplication is performed does not change the result.
The third property is that multiplication is distributive over addition. Say we had the expression \(5 \times (2 + 3)\). Note that whatever is inside the parenthesis must be evaluated first per the rule we defined earlier. This would then evaluate to \[5 \times (2+3) = 5 \times 5 = 25.\] Now instead of doing this, we could "distribute" the \(5\) into the parentheses and then add the result. This would look like \[5 \times (2+3) = 5 \times 2 + 5 \times 3.\] Before continuing, you may be wondering if the multiplication comes first or the addition. The short answer is mulitplication always comes before addition. This is a fundemental definition in mathematics that cannot be proven. It is known as an axiom, which is just a statement that is taken to be true without proof or justification. Since now we know that mulitplication comes before addition, let's put parentheses around the mulitplication operations to emphasize this. We now have, \[(5 \times 2) + (5 \times 3) = 10 + 15 = 25.\] Thus we see that the distributive property works.
The fourth property is the identity property. It says that any number multiplied by \(1\) is itself. For example, \[20 \times 1 = 20.\]
The fifth property is the zero property. It says that any number multiplied by \(0\) is \(0\). If this property seems unintuitive, then take it as a definition/axiom.
The sixth property is the negation property. It says that any number multiplied by \(-1\) is the negative version of itself. For example, \[20 \times -1 = -20.\]
As a side note, numbers multiplied together are called factors. So if we have the expression \(4 \times 5\), then \(4\) and \(5\) are factors. On the other hand, numbers added together are called terms. So if we have the expression \(4+3\), then \(4\) and \(3\) are terms. Many students who study arithmetic will memorize what is known as a multiplication table of the first ten positive integers since they are so common. The table is shown below.
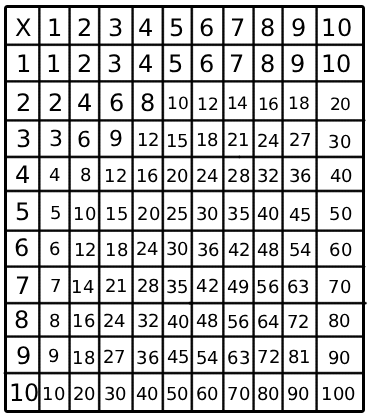 The properties stated above will aid us in building a strong foundation in algebra.
The properties stated above will aid us in building a strong foundation in algebra.
Division
Division can be thought of as how many times one number can fit into another number. Consider the number \(10\). How many times does the number \(5\) fit into \(10\)? If you said \(2\) you would be correct. This is because \(5+5=10\) or \(5 \times 2 = 10\). This is the basic law of division. We shall denote